Rumus Person Product Moment (PPM)

Uji Korelasi Pearson. 

Banyak penelitian meminati keberadaan hubungan antara 2 atau lebih variabel. Korelasi adalah suatu ukuran hubungan linier antar variabel. Contoh, peneliti ingin melihat apakah terdapat hubungan antara Minat Mahasiswa atas Matakuliah Pengantar Ilmu Politik (x) dengan Minat Mahasiswa untuk Berpolitik Praktis (y).

A. Pengantar
Banyak penelitian meminati keberadaan hubungan antara 2 atau lebih variabel. Korelasi adalah suatu ukuran hubungan linier antar variabel. Contoh, peneliti ingin melihat apakah terdapat hubungan antara Minat Mahasiswa atas Matakuliah Pengantar Ilmu Politik (x) dengan Minat Mahasiswa untuk Berpolitik Praktis (y). Potret Indonesia Kedua variabel tersebut, x dan y, bisa berhubungan dengan salah satu dari 3 cara berikut : 1. Hubungan Positif. Artinya, semakin berminat seorang mahasiswa atas Matakuliah Pengantar Ilmu Politik, semakin besar minat mereka untuk Berpolitik Praktis. 2. Tidak Ada Hubungan. Artinya, minat mahasiswa atas matakuliah Pengantar Ilmu Politik tetap sama kendati mereka berminat untuk Berpolitik Praktis. 3. Hubungan Negatif. Artinya, semakin mahasiswa berminat atas matakuliah Pengantar Ilmu Politik, semakin tidak berminat mahasiswa untuk Berpolitik Praktis. Cara termudah guna melihat apakah dua variabel berhubungan adalah dengan melihat apakah mereka memiliki covarians. Pemahaman atas covarians menuntut kita memahami konsep varians. Varians suatu variabel mewakili rata-rata perbedaan data variabel tersebut dengan nilai Mean-nya. Rumus varians sebagai berikut :

Mean sampel diwakili

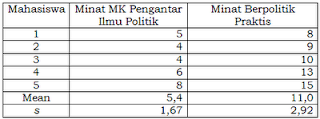
adalah nilai yang hendak dicari dan N adalah jumlah pengamatan (sampel). Jika kita tertarik apakah kedua variabel berhubungan, maka kita harus melihat apakah perubahan di satu variabel disusul dengan perubahan di variabel lainnya. Kala satu variabel menyimpang dari Mean, maka kita bisa berharap bahwa variabel lain juga menyimpang dari Mean-nya dengan cara serupa. Agar lebih jelas, lihat data berikut :

Jika terdapat hubungan di antara kedua variabel, maka kala satu variabel menyimpang dari Mean diikuti penyimpangan yang sama oleh variabel lainnya, baik searah atau berlawanan. Rumus covarians sebagai berikut :

Menghitung covarians adalah cara yang baik guna menilai apakah 2 variabel punya hubungan. Jika nilai covarians positif maka kala satu variabel menyimpang dari Mean diikuti oleh penyimpangan pada variabel lain secara searah. Jika nilai covarians negatif maka kala satu variabel menyimpang dari Mean diikuti oleh penyimpangan variabel lain secara berlawanan. Namun, covarians ini bukan uji standar guna menentukan hubungan.

B. Standardisasi 

Masalah uji standar bagi hubungan antar variabel diselesaikan lewat konversi. Artinya, covarians dikonversikan ke dalam unit yang lebih standar. Proses ini dinamakan standardisasi. Dalam kajian statistik, ukuran standar ini adalah Standar Deviasi. Jika kita membagi setiap penyimpangan nilai observasi terhadap Mean dengan Standar Deviasi, maka kita akan mendapat jarak dalam satuan Standar Deviasi. Singkatnya, jika kita ingin mengekspresikan covarians ke dalam unit standar pengukuran, kita tinggal membaginya dengan Standar Deviasi. Dengan demikian jika terdapat 2 variabel, maka akan terdapat 2 Standar Deviasi. Kini, kala kita hendak menghitung covarians, sesungguhnya kita menghitung 2 penyimpangan lalu mengkalikan mereka. Lalu, kita melakukannya secara sama terhadap Standar Deviasi. Kita mengkalikan mereka dan membaginya dengan hasil perkalian ini. Covarians yang sudah distandardisasi dinamakan Koefisien Korelasi. Rumusnya sebagai berikut :

Rumus di atas dikenal dengan nama korelasi Pearson Product-Moment atau Pearson Correlation Coefficient dan ditemukan oleh Karl Pearson. Jenis lain uji korelasi yang populer digunakan adalah Spearman Rank Correlation (rho). Uji statistik korelasi ini banyak digunakan untuk statistik nonparametrik yang datanya tidak berdistribusi normal dan diukur menggunakan skala ordinal. Tulisan ini hanya akan membahas uji korelasi Pearson Product Moment.

C. Rumus Pearson Product Moment 

Adapun rumus Pearson Product Moment (r) adalah sebagai berikut di bawah ini :

Lihat tabel di bawah ini dalam perhitungan korelasi Pearson :

Cara melakukan perhitungan manual untuk uji korelasi di atas adalah sebagai berikut:

D. Asumsi Uji Korelasi 

Sebelum diimplementasi, uji Korelasi terlebih dulu harus memenuhi serangkaian asumsi. Asumsi-asumsi uji Korelasi adalah : 1. Normalitas. Artinya, sebaran variabel-variabel yang hendak dikorelasikan harus berdistribusi normal. 2. Linearitas. Artinya hubungan antara dua variabel harus linier. Misalnya ditunjukkan lewat straight-line. 3. Ordinal. Artinya, variabel harus diukur dengan minimal skala Ordinal. 4. Homoskedastisitas. Artinya, variabilitas skor di variabel Y harus tetap konstan di semua nilai variabel X.

E. Cara Uji Asumsi Korelasi dengan SPSS Normalitas. 

Uji Normalitas bisa dilakukan dengan teknik Kolmogorov-Smirnov. Data yang normal adalah Sig. Kolmogorov-Smirnov hitung > Sig. Penelitian (0,05). Cara melakukan uji normalitas dengan SPSS adalah : 1. Klik Analyze --> Nonparametric Tests --> 1-Sample K-S. 2. Pada jendela One-Sample Kolmogorov-Smirnov Test, masukkan variabel x1, x2, x3, x4, dan y ke kota Test Variable List. 3. Pastikan sudah terceklis Normal pada Test Distribution. 4. Klik OK. Linieritas. Linieritas terlihat apabila skor variabel X meningkat, skor variabel Y juga meningkat. Plot-plot data cenderung mengikuti garis diagonal Z yang menaik. Uji asumsi dengan SPSS sangatlah mudah, caranya adalah : 1. Klik Graphs --> Scatter/Dot... 2. Klik icon Simple Scatter 3. Klik Define untuk membuka jendela Simple Scatter plot. 4. Masukkan variabel Y ke Y Axis ---> Masukkan variabel X ke X Axis. 5. Klik Options --> Ceklis Exclude cases listwise. 6. Klik Continue 7. Klik OK. Ordinal. Masih terdapat sejumlah perdebatan diantara para ahli apakah skala sikap (misal: sangat setuju, setuju, agak setuju, kurang setuju, tidak setuju, sangat tidak setuju) masuk kategori ordinal atau interval. Juga, uji Pearson apakah layak ditimpakan pada skala Interval dan Rasio ataukah minimal Ordinal bisa menggunakannya. Robert Ho menyatakan bahwa skala Ordinal pun layak ditimpakan uji korelasi Pearson. Mengenai apakah skala sikap masuk ke dalam kategori skala Ordinal atau Interval, Donald P. Schwab menjawab bahwa skala sikap boleh dimasukkan ke dalam skala Interval. Atau, jika tidak bisa, sekurangnya “mendekati Interval.” Schwab memutuskan, dengan demikian uji-uji statistik yang diperuntukkan bagi skala Interval bisa ditimpakan kepada yang “mendekati interval” tersebut. Homoskedastisitas. Dalam menguji asumsi Homoskedastisitas dilakukan secara grafis. Dengan SPSS hal ini sangat mudah. Caranya adalah sebagai berikut : Caranya dengan melihat grafik persilangan SRESID dengan ZPRED pada output hasil SPSS. Caranya sebagai berikut : 1. Klik Analyze --> Regression --> Linear 2. Masukkan variabel y ke Dependent. 3. Masukkan variabel-variabel x ke Independent(s) 4. Klik Plot. 5. Isikan SRESID pada y-axis dan ZPRED pada x-axis. 6. Klik Continue. 7. Saksikan hasilnya pada Output SPSS. Perhatikan grafik scatterplot. Ingat, Homoskedastisitas terjadi jika varians dari residual satu pengamatan ke pengamatan lain tetap atau sama. Heteroskedastisitas terjadi jika varians dari residual satu pengamatan ke pengamatan lain tidak sama atau tidak tetap. Homoskedastisitas terjadi jika tidak terdapat pola tertentu yang jelas, serta titik-titik menyebar di atas dan di bawah angka 0 pada sumbu X. Heteroskedastisitas terjadi jika terdapat titik-titik memili pola tertentu yang teratur seperti bergelombang, melebar kemudian menyempit.

F. Uji Korelasi Pearson dengan SPSS 

Melakukan uji Korelasi Pearson untuk mencari nilai r dengan SPSS sangatlah mudah. Caranya sebagai berikut : 1. Klik Analyze --> Correlate --> Bivariate 2. Klik Masukkan variabel x1, x2, x3, dan y ke kotak Variables. 3. Pada bagian Correlation Coefficients, ceklis Pearson. 4. Pada bagian Test of Significance, ceklis Two-tailed. 5. Klik Options --> Ceklis Means and standard deviations --> Ceklis Exclude cases pairwise. 6. Klik Continue. 7. Klik OK. 8. Saksikan hasilnya pada Output SPSS. Contoh Output Hasil SPSS sebagai berikut :

Hipotesis penelitian adalah : G. Interpretasi Hasil Uji Korelasi Penelitian (contoh) hendak menguji apakah terdapat hubungan antara Budaya Organisasi (x1) dan Iklim Organisasi (x2) dengan Kepuasan Kerja (y). Hasil uji statistik menggunakan Pearson Product Moment (sudah tertera di atas). Bagaimana melakukan penafsiran? Korelasi. Jika suatu hubungan tidak sama dengan 0, maka dapat dikatakan terjadi hubungan. Perhatikan baris-baris Pearson Correlation, di mana dihasilkan hasil-hasil berikut : • Budaya Organisasi berhubungan secara positif dengan Kepuasan Kerja sebesar 0,451 (r = 0,451). • Iklim Organisasi berhubungan secara positif dengan Kepuasan Kerja sebesar 0,838 (r = 0,838). Dengan demikian, terdapat hubungan antara variabel x1 dan x2 dengan y. Hipotesis-hipotesis 0 di atas, sebab itu, ditolak. Signifikansi. Signifikansi bisa ditentukan lewat baris Sig. (2-tailed). Jika nilai Sig. (2-tailed) < 0,05, maka hubungan yang terdapat pada r dianggap signifikan. Hasil uji signifikansi (di atas) adalah : • Nilai r hubungan Budaya Organisasi dengan Kepuasan Kerja adalah 0,000. Artinya, 0,000 < 0,05 dan dengan demikian korelasi antara kedua variabel signifikan. • Nilai r hubungan Iklim Organisasi dengan Kepuasan Kerja adalah 0,000. Artinya, 0,000 < 0,05 dan dengan demikian korelasi antara kedua variabel signifikan. Interval Kekuatan. Sejumlah penulis statistik membuat interval kategorisasi kekuatan hubungan korelasi. Jonathan Sarwono, misalnya, membuat interval kekuatan hubungan sebagai berikut :

Untuk korelasi negatif (-) interpretasi adalah sama. Koefisien Determinasi. Koefisien Determinasi digunakan untuk menafsirkan skor korelasi Pearson (r). Caranya dengan mengkuadratkan nilai r tersebut. Nilai r harus dikuadratkan karena ia bukan berada dalam skala Rasio. Akibatnya, kita tidak bisa melakukan operasi aritmetika (kurang, bagi, kali, tambah) terhadap nilai r tersebut. Guna mencari nilai Koefisien Determinasi, dilakukan langkah berikut : • Nilai r Budaya Organisasi – Kepuasan Kerja = 0,451 x 0,451 = 0,2034. Kalikan nilai ini dengan 100% maka 0,2034 x 100% = 20,34%. • Nilai r Iklim Organisasi – Kepuasan Kerja = 0,838 x 0,838 = 0,7022. Kalikan nilai ini dengan 100% maka 0,7022 x 100% = 70,22. Penafsiran Koefisien Determinasi adalah : • Sebesar 20,34% varians Kepuasan Kerja dapat dijelaskan oleh Budaya Organisasi. • Sebesar 70,22% varians Kepuasan Kerja dapat dijelaskan oleh Iklim Organisasi. ---------------------------------

DAFTAR PUSTAKA 

Andi Field, Discovering Statistics using SPSS: And Sex Drug and Alcohol, Second Edition (London: SAGE Publication, 2005)
Donald P. Schwab, Research Methods for Organizational Studies, Second Edition (New Jersey: Lawrence Erlbaum Associates, Publishers, 2005)

Jonathan Sarwono, Statistik Itu Mudah: Panduan Lengkap untuk Belajar Komputasi Statistik Menggunakan SPSS 16 (Yogyakarta: Penerbit Universitas Atma Jaya Yogyakarta, 2009).

Mark R. Leary, Introduction to Behavioral Research Methods, Third Edition (Boston: Allyn and Bacon, 2001)

Muhammad Nisfiannoor, Pendekatan Statistika Modern untuk Ilmu Sosial (Jakarta: Penerbit Salemba Humanika, 2009)

Robert Ho, Handbook of Univariate and Multivariate Data Analysis and Interpretation with SPSS (Boca Raton: Chapman & Hall/CRC, 2006) p. 184.